The principle of stationary action allows derivation of conservation laws from transformation properties of the Lagrangian. From this, energy, momentum, angular momentum, and other quantities that may be conserved, are given formulations that depend only on the Lagrangian, coordinates, and time. Thus, concepts such as energy, momentum, and angular momentum gain well-defined meaning for any physical system that has a Lagrangian. Since every physical theory can be described by the principle of stationary action, the concepts of energy, momentum, angular momentum and other conserved quantities are consistently defined for all these theories.
The Lagrangian arises naturally through an introductory example from geometry. We then utilize the formalism to reformulate NL2 in the form of the E-L equation. We also prove the invariance of the E-L equation under arbitrary coordinate transformations. To make clear why this property is important for physics, we remind ourselves that the law of nature do not depend on the coordinate we use to describe them. On the other hand physicists cannot formulate laws without coordinates and physical equations look different under different coordinates.
This is why the relation of physical theories to coordinates should be as well defined and restricted as possible. The Lagrangian formalism fulfills this demand through E-L equation being independent of coordinate transformations.
Lagrangian functionals do depend on coordinates, but in the simplest way physicists can think of: they transform like scalars.
Thinking about the relation of the laws of physics to coordinates proved fruitful in the past. Probably the most famous example is Einstein’s famous paper on special relativity.
We will reformulate NL2 in the form of E-L equations. As a result, the Lagrangian of classical mechanics appears naturally without further derivation.
The Lagrangian formalism and the minimal distance between two points in a plane
We show that the minimal distance between two points in a plane is a straight line.
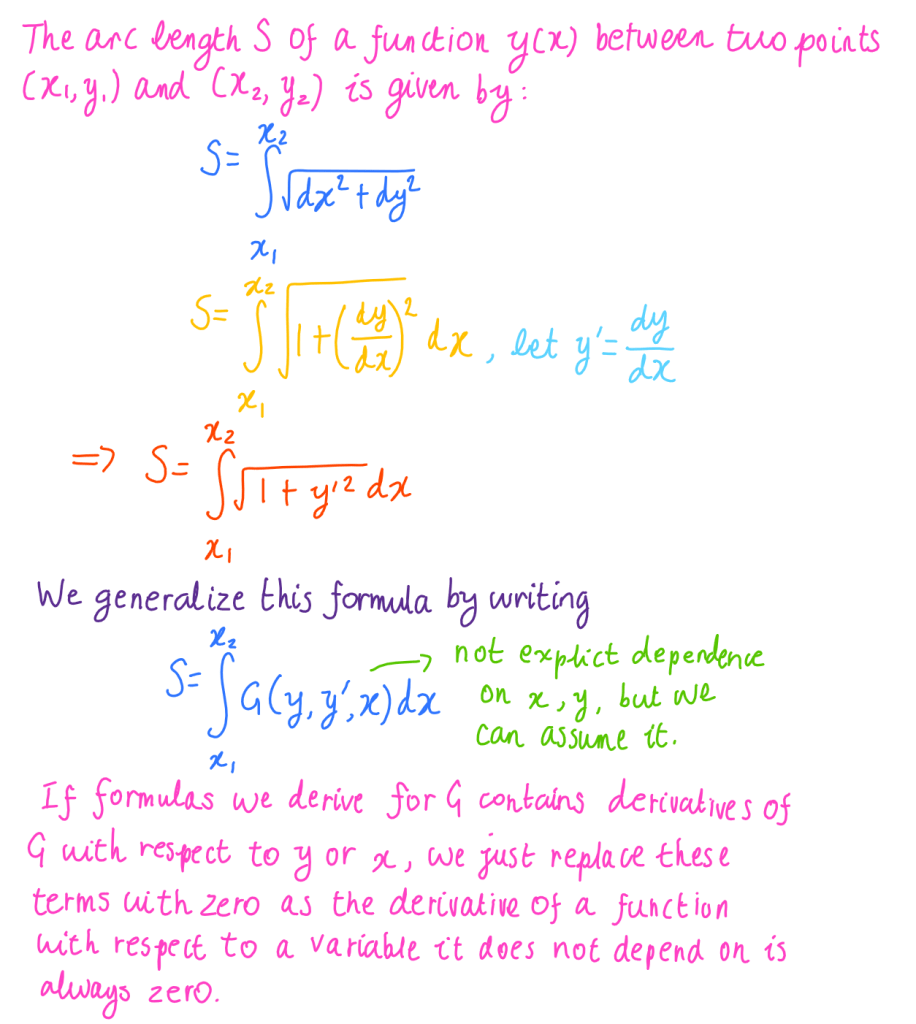

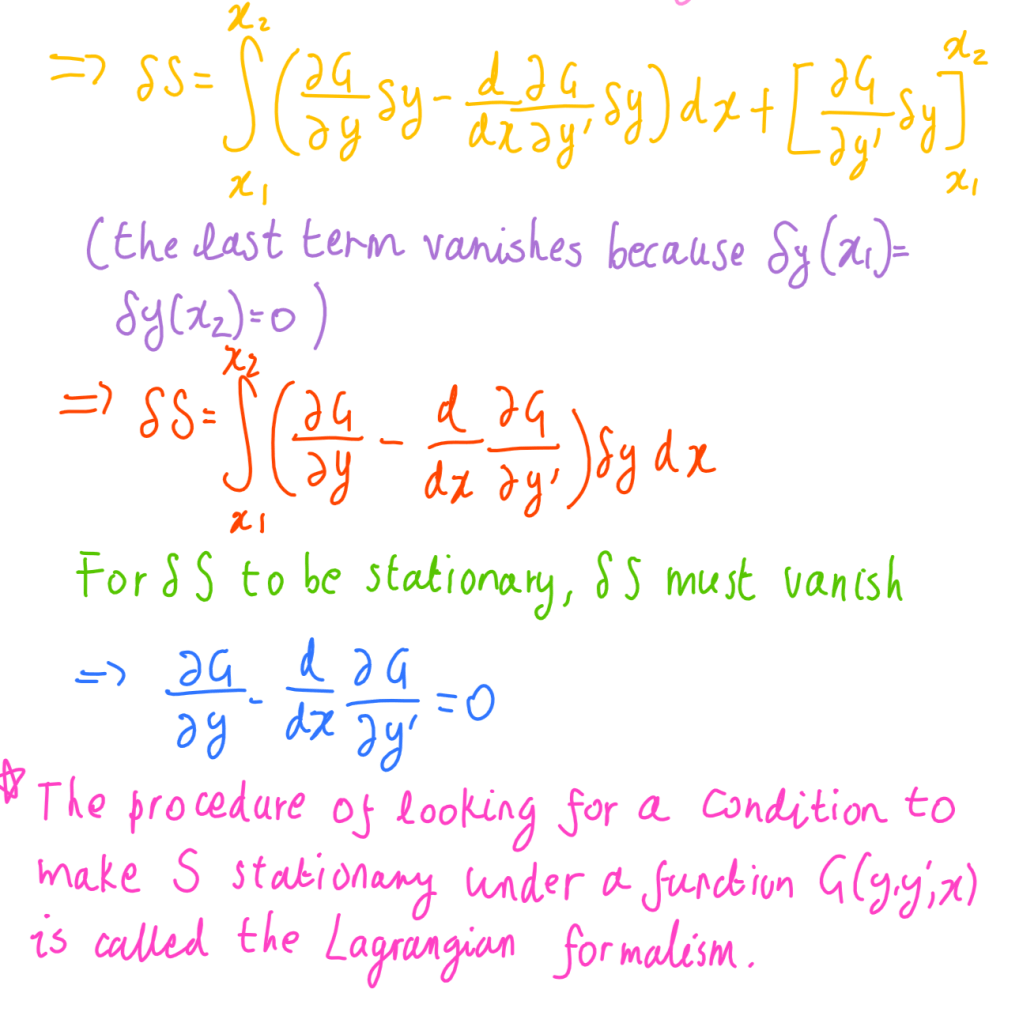
Application to Newtonian mechanics

Invariance of the E-L equation under coordinate transformations


